Cn Mod Xz
) and suppose that f T= f ae Let fhave Fourier series f(x) = X1 n=1 c ne 2ˇinx(in L2) For each p 0, f Tphas Fourier series X1 n=1 c ne.

Cn mod xz. If a 7 (mod 8) and b 3 (mod 8), then there exists integers k;m such that a 7 = 8k and b 3 = 8m Then, ab 5 = (8k 7)(8m 3) 5 = 64km 56m 24k 21 5 = 8(8km 7m 3k 2) That is, ab 5 0 (mod 8), or ab 5 (mod 8) 16 Determine if each of the following statements is true or false Provide a counterexample for statements that are false and provide a complete proof for those that are. If x, z are negative and y is positive, then we can rearrange to get In other words, it was necessary to prove only that the equation a n b n = c n has no positive integer solutions (a, b, c) when n is an odd prime number This follows because a solution (a, b, c) for a given n is equivalent to a solution for all the factors of n For illustration, let n be factored into d and e, n = de. Notice that gn = ι, the identity permutation Since g ∈ Aut(C n) then the cyclic group R = {gm 0 ≤ m ≤ n−1} of order n is a subgroup of Aut(C n) If h is the element of the symmetry group S n = Sym(n) which maps i to −i(mod n), then h.
Problem If a 2Z and a 1 (mod 5), then a2 1 (mod 5) 3 Proof Assume that a 2Z and a 1 (mod 5) By de nition of congruence modulo 5 this implies that 5 divides a 1 which further implies that there exists some k 2Z such that a 1 = 5k so a = 5k 1 It follows that a = 5k 1 a3 = (5k 1)3 a 3= 125k 75k2 15k 1 a3 31 = 125k 75k2 15k a 3 1 = 5(25k 15k2 3k) Hence 5 divides a 3 1. MATH 00 Assignment 3 Solutions 1 a) List of tautologies and equivalences see class handout, also posted on course webpage b) Define the meaning of any of the 10 axioms for the set of integers see class. 1, which again implies that an!0.
Stack Exchange network consists of 176 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange. 02/07/15 · Free Online Scientific Notation Calculator Solve advanced problems in Physics, Mathematics and Engineering Math Expression Renderer, Plots, Unit Converter, Equation Solver, Complex Numbers, Calculation History. 25/09/13 · This mod will allow you to save structure data from a 152 world so that it can be loaded with the new structure saving and loading algorithm.
Z 2n = e−z2/ 4 Use the comparison test to show that the following series converge (a) X∞ n=1 sin(√ 2nπ) 2n (b) X∞ n=1 n2 −n−1. 846 Let R be the relation de ned by Z by a R b if a b 0 (mod 3) Show that R is not an equivalence relation Solution R is not an equivalence relation It is not re exive, since, for example, 1 1 = 2, which is not congruent to 0 (mod 3), and so we do not have 1 R 1 850 A relation R is de ned on Z by a R b if 2a 2b 0 (mod 4) Prove. (fx)z −(fz)x j (fy)x −(fx)y k = (0,0,0) = 0, and (ii), curl(fF) = i j k ∂ ∂x ∂ ∂y ∂ ∂z fF1 fF2 fF3 = (fF3)y −(fF2)z i (fF1)z −(fF3)x j (fF2)x −(fF1)y k = f (F3)y −(F2)z i (F1)z −(F3)x j (F2)x −(F1)y k (fyF3 −fzF2)i(fzF1 −fxF3)j(fxF2 −fyF1)k = f curlF x i j k f fy fz F1 F2 F3 = f curlFgradf × F, as required Example 413 Let F= (x2y,yz,xz) Find (i).
Whence x3 x • 0 ¥ Problem 8 A circle has center (2;4) (a) Prove that (¡1;5) and (5;1) are not both on the circle (b) Prove that if the radius is less than 5, then the circle does not intersect the line y = x¡6 Solution (a) It suffices to. Hmod Following ArakawaSuzuki, if Xis any U(g) module, there is a natural H = S(V_) CW action on X z }n {(Cn Cn) The Waction is obvious The action of e iin Cn’V_,!S(V_) ,!H involves Xand the ith copy of Cn e i7!. N = Sym(n) which maps i to (i 1)(mod n), then g ∈ Aut(C n) (as is easily verified) Notice that g is an elementary rotation of the cycle C n;.
Problem 7 Write a proof by contraposition to show that for any real number x;. /12/ · PREVIEW ACTIVITY \(\PageIndex{1}\) Sets Associated with a Relation As was indicated in Section 72, an equivalence relation on a set \(A\) is a relation with a certain combination of properties (reflexive, symmetric, and transitive) that allow us to sort the elements of the set into certain classes. A b 2y 22Z, x z is even and so xRz Therefore, R is transitive The distinct equivalence classes of R are 0 = fx 2Z x is eveng 1 = fx 2Z x is oddg We see that these are the only distinct equivalence classes of R because we have proven that for the sum of two numbers to be even, they both must have the same parity, and for x 2Z, x2 is even/odd if and only if x is even/odd So, 0.
Problem4(WR Ch 3 #11) Suppose an ¨0, sn ˘a1 ¯¢¢¢¯an, and P an diverges (a) Prove that P a n 1¯an diverges Solution Assume (by way of contradiction) that P a n 1¯an converges Then an 1¯an!0 by Theorem 323 Since an 6˘0, we can divide the top and bottom of this fraction by an to get 1 1 an ¯1!. An abstract group defined by this multiplication is often denoted C n, and we say that G is isomorphic to the standard cyclic group C n Such a group is also isomorphic to Z/nZ, the group of integers modulo n with the addition operation, which is the standard cyclic group in additive notation Under the isomorphism χ defined by χ(g i) = i the identity element e corresponds to 0,. The notation ‘x ≡ y mod n’ is used to denote the congruence of integers x and y modulo n One can readily verify that congruence modulo the given integer n is an equivalence relation on the set Z of all integers x ≡ x mod n for all integers x (the relation is reflexive);.
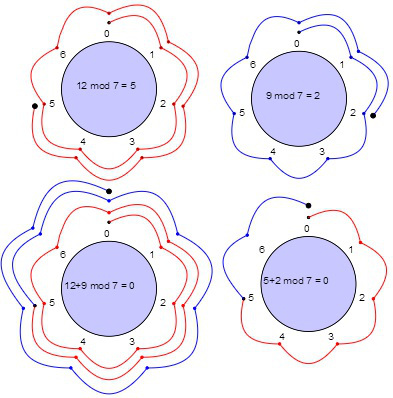
Thisisnonobvious Consider themapRP 2!S thatpinchesRP1 toapoint NowH 2(RP2;Z) = 0,soinH 2 thismapiszero ButinZ=2Zcoefficients,indimension2,thismapgivesanisomorphism Thisshowsthatthere’s no functorial determination of H (X;Z=2) in terms of H (X;Z);. (c) X∞ n=0 (−1)n 2nn!. If we denote the rotation by angle θ about (x z)/ 2 by R() ψ = ∑ x modN A ⊗ 3 modx N B ⊗ 5 modx N C N x=0 Find the output state if we take a quantum Fourier transform modulus N on each of the registers A, B, and C That is, if we denote the corresponding QFT operators to each system by U, U B, A and U C, find UUU⊗ C ψ Write your answer in the basis {0,1,, N − 1}⊗3.
2i, (c) n i=1 in, (d) X2n i=n i 3 In a proof by induction that 6n −1 is divisible by 5, which result may occur in the inductive step (let 6k −1 = 5r)?. Show That C1 Is Asubgroup Of Z X Z(b) For Each Positive Integer N2, Let Cn = {(Cn ={(a, B) Z X Za B (mod N)}Show That Cn Is A Subgroup Of Z X Z(c) Show That Every Subgroup Of Z XZ That Contains C1 Has The FormCn, For Some Positive Integer N. Search through millions of guided stepbystep solutions or ask for help from our community of subject experts 24/7 Try Chegg Study today!.
Get homework help fast!. F (g;K)mod !. Is degree n 1, c n 6= 0 But c n is also the coe cient on the highestdegree term, xn 1, in g(x), so g(x) is degree n 1, as desired Part 52 For each real a, the function p given by p(x) = f(x a) is a polynomial of degree n Solution We induct on n to prove this statement4 Base Case We could use n = 0 as the base case, but for clarity.
Integer multiplication respects the congruence classes, that is, a ≡ a' and b ≡ b' (mod n) implies ab ≡ a'b' (mod n) This implies that the multiplication is associative, commutative, and that the class of 1 is the unique multiplicative identity Finally, given a, the multiplicative inverse of a modulo n is an integer x satisfying ax ≡ 1 (mod n) It exists precisely when a is coprime. Z c up conversion if Z I Z c down conversion Department of Electrical and Computer Engineering 2(Z c Z I)t m(t)(Z ct) Signal with a carrier frequency Frequency Converted Signal Bandpass Filter Option 1 x(t) m(t) (Z c t)2 (Z c Z I)t m(t) 2 cos(Z c t) cos(Z c Z I)t m(t (Z I t) (2Z c Z I)t x(t. Mod (Z) Z Z c 2 1 Z c B Z c B Z B Z c B The Goal is to change to Z I m(t)(Z c t) o m( Z It) if Z I!.
Theorem 12 The Fundamental Theorem of Arithmetic Every integer greater than 1 can be written uniquely in the form pe 1 1 p e 2 2 ···p e k k, where the p i are distinct primes and the e i are positive integers Theorem 13. 27/09/15 · k 4 mod 6 for all positive k, which also means that a k1 4 mod 6 for all positive k Let a 99 = 4 6t for some integer t Then, 1 a 100 4a 99 446t 44(46)t 256 46 4 mod 7 (Actually a n 4 mod 7 for all n 1) 8 Solve the congruence x103 4 mod 11 Solution x 5 mod 11 By Fermat’s Little Theorem, x10 1 mod 11 Thus, x103 x3 mod 11 So, we only need to solve x3 4 mod 11 If we try. Proposition 317 If a and m are coprime, then the equation ax ≡ b (mod m) has a unique solution x (mod m) Proof As a and m are coprime there exist u,v with au mb = 1 Thus aub vmb = b Hence x ≡ ub (mod m) is a solution to ax ≡ b (mod m) To show that this solution is unique, consider the map φ Z/(m) → Z/(m) defined by φ(x.
This program prints on screen the final values of a and b (4 and 7, respectively) Notice how a was not affected by the final modification of b, even though we declared a = b earlier Assignment operations are expressions that can be evaluated That means that the assignment itself has a value, and for fundamental types this value is the one assigned in the operation. (mod n) so you can multiply the exponent by two by doing one multiplication In general, write b= c m m2 c m 1 2m 1 c 12 c 0 where c i 2f0;1g Then compute a;a2;a4;;a2 m (mod n) by multiplying the previous element in this list with itself This takes m 1 multiplications Finally compute ac m2 m ac m 12 m 1a2c 1 ac 0 ab (mod n) This requires at most mmultiplications, as. This generalizes the examples above Conversely, every sequence generated by a fraction of polynomials satisfies a linear recurrence with constant coefficients;.
This video was uploaded from an Android phone. C ne 2ˇinx then the RiemannLebesgue lemma tells us that c n!0 as n!1 Proposition 45 The doubling map T X!Xde ned by T(x) = 2xmod 1 is ergodic with respect to Lebesgue measure Proof Let f2L2(X;B;. Then x > 0 Solution Suppose x • 0 Then x3 • 0;.
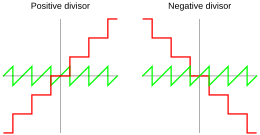
The Kawasaki C2 is a long range twinengine transport aircraft In comparison with the older C1 that it replaces, the C2 can carry payloads up to four times heavier, such as MIM104 Patriot surfacetoair missile batteries and Mitsubishi H60 helicopters, and possesses six times the range The C2 is being developed to meet the following requirements of the Ministry of Defense a. Set Symbols A set is a collection of things, usually numbers We can list each element (or "member") of a set inside curly brackets like this Common Symbols Used in Set Theory Symbols save time and space when writing. 9 the multiplication of 3 by 4 results in 3 since 12 ≡ 3 mod 9,and therefore 12 is identified with 3 Z n is a ring,which is an integral domain (and therefore a field,sinceZ n is finite) if and only if nis prime For if n= rsthen rs=0inZ n;ifnis prime then every nonzero element in Z n has a multiplicative inverse,by Fermat’s little theorem 134 Note that by definition of.
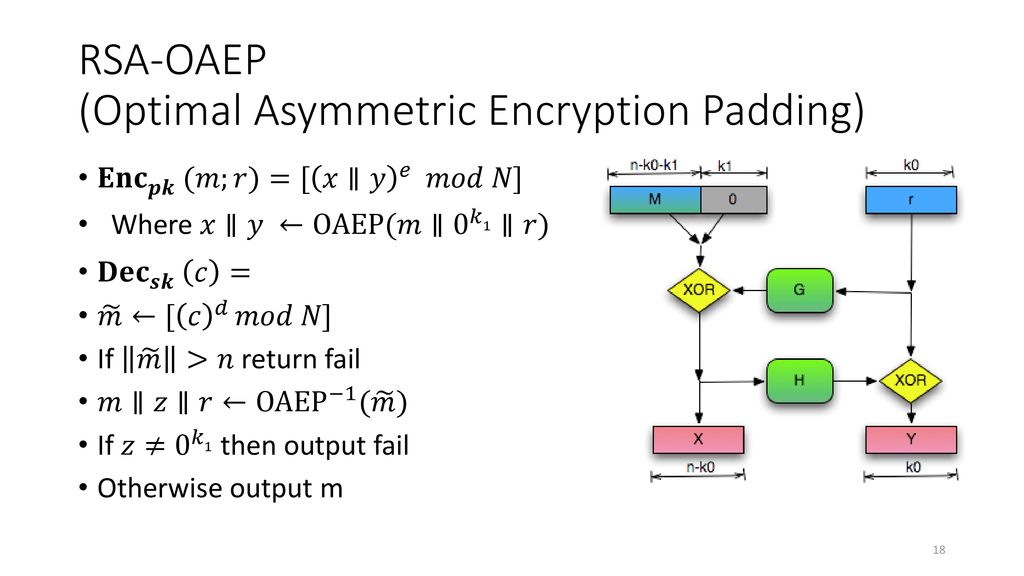
0, which implies that 1 an!. Then by de nition b a (mod n) By the transitivity property of congruence we then have a b (mod n) and a c (mod n) ) b c (mod n) So b 2c n Thus, any element b of a n is also an element of c n Reversing the roles of a and c in the argument above we similarly conclude that any element of c n is also an element of a n Therefore a. FullyHomomorphicEncryption Examples homomorphicschemes Multiplicativelyhomomorphic RSA c 1 = me 1 mod N et c 2 = me2 mod N Eval(c 1,c 2) = c 1c 2 = (m 1m 2) e mod N= E(m 1m 2) mod N Additivelyhomomorphic Paillier c 1 = gm1rn 1 mod n 2 et c 2 = gm2rn 2 mod n 2.
7 Kummer congruences Theorem 71 Let c ∈Q be prime to Np Then E(N) k,c (x) ≡xk−1E(N) 1,c (x) mod N kD(k) Z p We may assume that x is an integer,. Which have the form y0= f 0(x) f 1(x)y f 2(x)y2 for some f 0,f 1,f 2 ∈K(x), can be consideredasthesimplestformofnonlinearAODEs In13,Kovacicgivesacomplete. 2 1 Sets and Functions Sets are determined entirely by their elements Thus, the sets X, Y are equal, written X= Y, if x2X if and only if x2Y It is convenient to de ne the empty set, denoted by ?, as the set with no elements.
If x ≡ y mod n and y ≡ z mod n then x ≡ z. If x ≡ y mod n then y ≡ x mod n (the relation is symmetric);. The ordinary generating function of a sequence can be expressed as a rational function (the ratio of two finitedegree polynomials) if and only if the sequence is a linear recursive sequence with constant coefficients;.
Ma ≡ 1(mod n) In terms of , we have m a = 1 Thus, a has a multiplicative inverse in Z n As a consequence of the above theorem we have Theorem 126 Every nonzero element of Z n has a multiplicative inverse if and only if n is a prime number Thus, (Z∗ n, ) is a group if and only if n is prime Proof Suppose first that a has a multiplicative inverse for all 1 ≤ a < n Then. − x mod p as polynomials (all coefficients mod p) Proof Suppose f(x) has n solutions Then n ≤ p because only p possible roots mod p (ie, deg(f) ≤ deg(x p − x)) Divide x p − x by f(x) to get x p − x = f(x)g(x) r(x), deg(r) < deg(f) = n Now note, if α is a root of f(x) mod p then plug in to get α p − α = f(α)g(α) r(α) ≡ 0g(α) r(α) ≡ r(α) mod p so α. (NB you may need to rearrange your equation) (a) 6k1 −1 = 5(6r −1), (b) 6k1 −1 = 6(5r 1), (c) 6k1 −1 = 5(6r 1), (d) 6k1 −1 = 5×6r 7 End Quiz Solutions to Exercises 15 Solutions to Exercises Exercise 1(a) The sum.
22 Limits and continuity The absolute value measures the distance between two complex numbers Thus, z 1 and z 2 are close when jz 1 z 2jis smallWe can then de ne the limit of a complex function f(z) as follows we write. Particular, it is easy to show that x(z) mod u(z) = x(z) mod u(z)v(z) mod u(z) for any u(z)and v(z) This means that we can first compute x(z) modulo the product of the factors, and then recursively evaluate the remainder by a recursive factorization of this product But the product Q k(z − e− 2πi N k) = zN − 1, since the e− 2πi N. Free Online Integral Calculator allows you to solve definite and indefinite integration problems Answers, graphs, alternate forms Powered by WolframAlpha.
(c) n(n−1) rn2 (d) n(n5) rn2 The equation ∇2f = 0 is called Laplace’s equation This is an important equation in science From the above exercises and quiz we see that f = 1 r is a solution of Laplace’s equation except at r = 0 Section 2 The Laplacian 7 The Laplacian of a scalar field can also be written as follows ∇2f = ∇·∇f ie, as the divergence of the gradient of f. If x3 x > 0;. The effect of a map in integral homology does not determine its effect in mod.
X j E j acting on X E j acting in ithcomponent where the sum is over any selfdual orthonormal basis fE. Spring 18 Intro to Lattice Algs & Crypto Homework 1 Due 10/04/18 D Dadush, L Ducas Mastermath Exercise 1 (Fun with lattices pts) 1Construct an explicit basis for the lattice fx 2Zn x 1 ån i=2 a ix i 0 (mod p)g, where a i 2 Z/pZ, p a prime 2For all large enough n 2Z, find an ndimensional fullrank lattice Lin which vectors v. X 5 ≡ x (mod 5) y 5 ≡ y (mod 5) z 5 ≡ z (mod 5) and therefore x y z ≡ 0 (mod 5) This equation forces two of the three numbers x, y, and z to be equivalent modulo 5, which can be seen as follows Since they are indivisible by 5, x, y and z cannot equal 0 modulo 5, and must equal one of four possibilities ±1 or ±2 If they were all.

Slides Show
Answered 1 Let F Z Z Defined By F 2 2 Bartleby

Primitive Root Modulo N Wikipedia
Cn Mod Xz のギャラリー

Complex Numbers Absolute Value

Modulus And Argument Of Complex Numbers What Is Modulus And Argument Of Complex Numbers Examples Solutions Cuemath

Presentation
Modulo Operation Wikipedia

Complex Numbers Absolute Value

Complex Number Wikipedia

Quiz A 答案直接寫於題目後 不夠寫在後面 姓名

Slides Show

Prove That The Relation X Y Mod N X Is Congruen Chegg Com

Pdf A Congruence With The Euler Totient Function

Chinese Remainder Theorem Wikipedia

Solved Observe That Mod And Div Can Be Defined As Functio Chegg Com
Modular Addition And Subtraction Article Khan Academy

Public Key Cryptography Ppt Download

Experiment 5 Programmer Sought
Topic 31 Rsa Attacks Fixes Ppt Download

Algorithmic Number Theory And Cryptography Cs 303 Modular Arithmetic Ppt Download

Security Public Key Cryptography Ppt Download

Solved Two A Prove That The Relation Y Mod N X Is Congr Chegg Com

Pdf A Note On Jesmanowicz Conjecture For Non Primitive Pythagorean Triples

Cyclotomic Polynomial Wikipedia

Solutions To Problem Set 4 Zoo Yale University
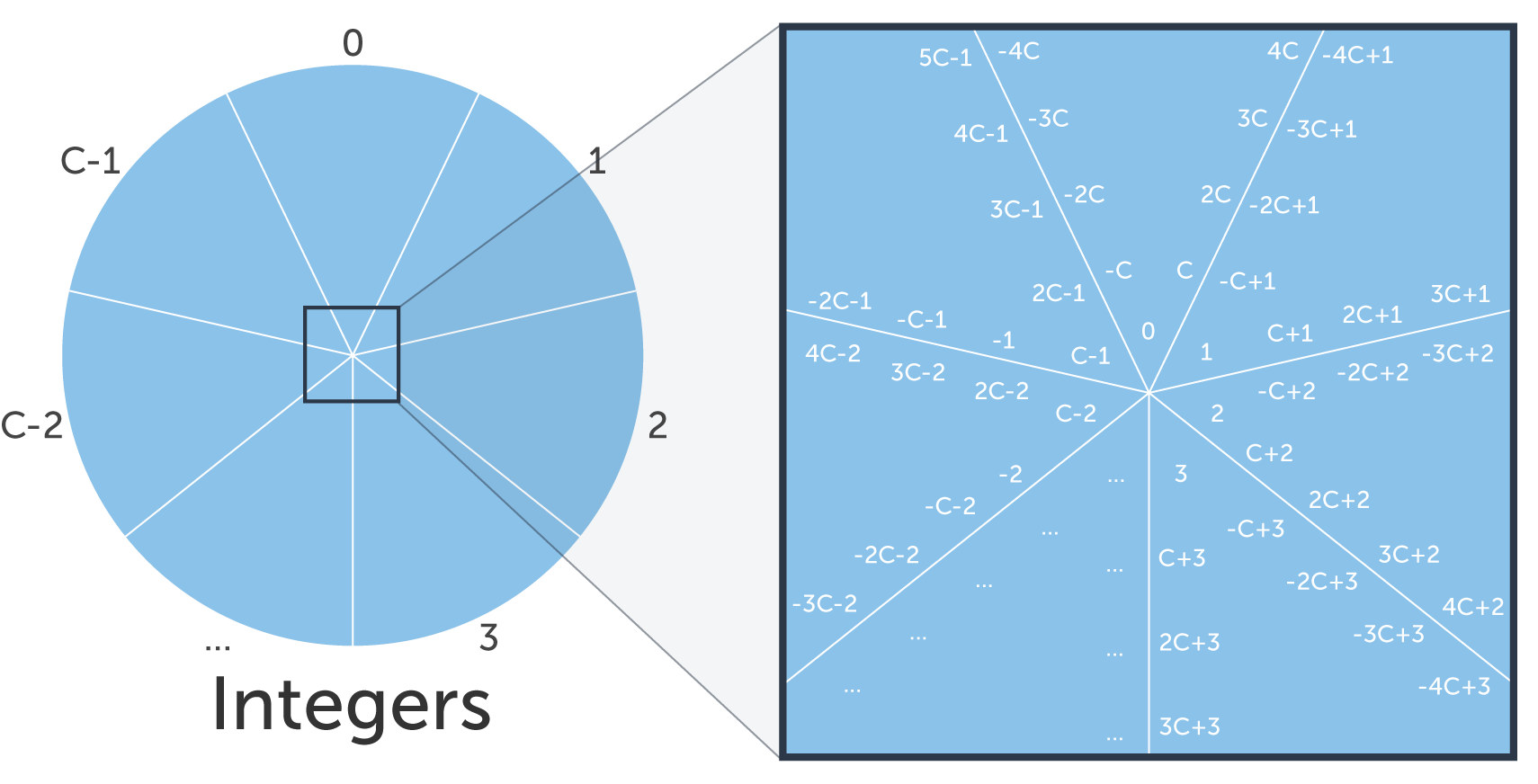
Congruence Modulo Article Cryptography Khan Academy
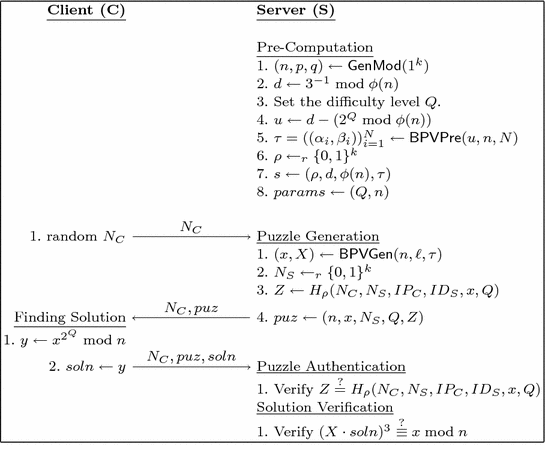
Improved Cryptographic Puzzle Based On Modular Exponentiation Springerlink

Numerical Algorithms Chapter Ppt Video Online Download
Problem 1 Points Let Pi Pr Where Pi Are Distinct Odd Primes And Denote By Z The Multiplicative Group Of Units In In That Is Ix Course Hero

Modulo Operation Wikipedia

Assignment 3 Version 1 3 Manualzz

Classical Cryptography Outline N 1 Introduction Some Simple
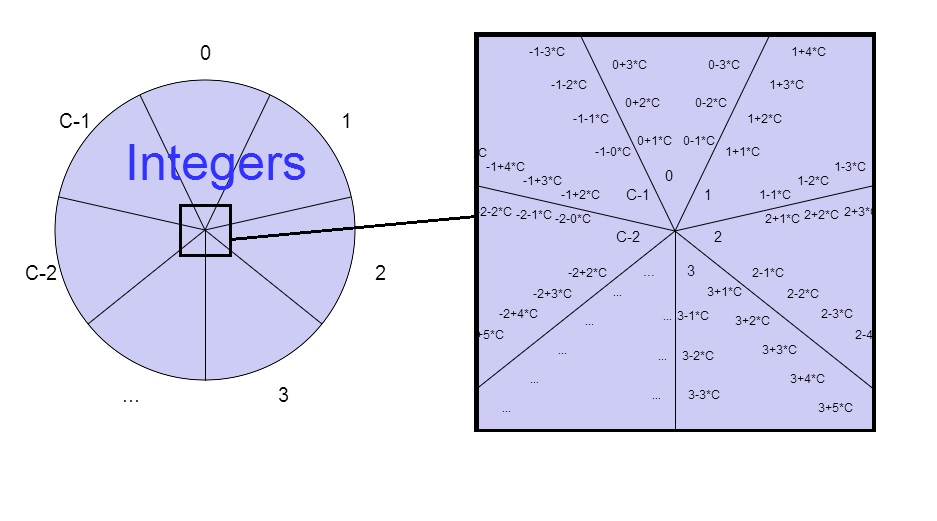
Equivalence Relations Article Khan Academy

15 251 Great Theoretical Ideas In Computer Science

Pdf Proof Of A Conjecture Involving Sun Polynomials

Solved 12 Let A B P K E Z A Prove That If P Is Pri Chegg Com
Modular Arithmetic Wikipedia

Solved Question 5 A Define A Relation R On The Set Of A Chegg Com

Chapter 4 More On Direct Proof And Proof By Contrapositive

Millionaire S Problem With Real Life Rsa Example

Algorithmic Number Theory And Cryptography Cs 303 Modular
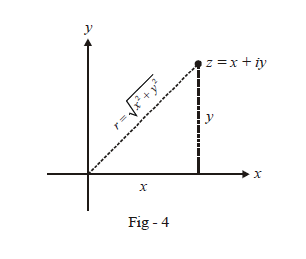
Modulus And Argument Of Complex Numbers What Is Modulus And Argument Of Complex Numbers Examples Solutions Cuemath

2 Let N Be Any Positive Integer Let C Be The Se Chegg Com

Solved Congruent Simplification 15 Pts 1 Z Congruent Modulo N Denoted Mod Defined Z V Remainder D Q

The Sum Of Digits Of Polynomial Values In Arithmetic Progressions Pdf Free Download

Public Key Cryptography And Rsa Review Number Theory Basics Pdf Free Download




